Table of Contents
Definition of Median:
Median of a set of values of a variable gives a measure of their central tendency and is defined to be the middle most variable value when the values are arranged in order of magnitude (ascending or descending).
In the words, Median is the value of that item in a series which divides the series into two equal parts, one part consisting of all values less and the other all values greater than it.
Thus, median is a positional average i.e., its value depends on the position occupied by a value in the series of observations. Median is the value of observation in the most central position ;
hence, it may be regarded as the real measure of central tendency of a distribution. An important property of median is that the sum of absolute deviations from median is minimum.
Calculation of Median:
(a) Simple Series (ungrouped data)
Procedure:
(i) Arrange the data in either ascending or descending] order of magnitude.
(ii) If the number of observations is odd, the value of the middle-most items is the median. However, if the number be even, the arithmetic mean of the two middle most item is taken as median.
When ‘ n ‘ is odd. In this case ![]() th value is the median. M=
th value is the median. M=![]() th term.
th term.
When ‘ n ‘ is even. In this case there are two middle terms. ![]() th and
th and ![]() th. The median is the average of these two terms.
th. The median is the average of these two terms.![]()
Example 1. Find the median of the following numbers:
(a) 21,12,49,37,88,46,55,74,63
(b) 88,72,33,29,70,86,54,91,61,57.
Solution: (a) Let us arrange the data in order: 12,21,37,46,49,55,63,74,88
In this data the number of item is n=9 (odd)
\therefore Median
=M=![]()
Now the 5 th value in the data is 49 .
Median is 49.
(b) Let us arrange the data in order: 29,33,54,57,61,70,72,86,88,91
In this data the number of item is n=10 (even)
Median = average of ![]() th +
th +![]() terms.
terms.
= Average of ![]() th and
th and ![]() th terms.
th terms.
= Average of 5 th and 6 th terms
= ![]()
(b) Grouped Data:-
1. Discrete series:
Procedure:
(i) Arrange the data in either ascending or descending order of magnitude.
(ii) A table is prepared showing the corresponding frequencies and cumulative frequencies,
(iii) Now median is calculated by the following formula
M=![]()
Example 1. Find the median for the following data:
Income | 100 | 150 | 80 | 200 | 250 | 180 | Total |
f | 24 | 26 | 16 | 20 | 6 | 30 | 122 |
Solution: let us arrange the income in ascending order and then from cumulative frequency
x | f | c.f. |
80 | 16 | 16 |
100 | 24 | 40 |
150 | 26 | 66 |
180 | 30 | 96 |
200 | 20 | 116 |
250 | 6 | 122 |
As n=122 (even), So the median (M)= average of ![]() th
th
=![]()
=![]()
61.5 th lies is the interval 41 to 66 . Therefore its value is 150 .
Example 2 Calculate the median
x | 20 | 25 | 50 | 9 | 80 | 40 |
f | 6 | 16 | 7 | 4 | 2 | 8 |
Solution: let us arrange the data ( marks) in ascending order and then from cumulative frequency
x | f | c.f. |
9 | 4 | 4 |
20 | 6 | 10 |
25 | 16 | 26 |
40 | 8 | 34 |
50 | 7 | 41 |
80 | 2 | 43 |
Here ![]()
Median (M) is ![]() nd value
nd value
The table shows that all items from 11 to 26 have their values 25 . Since 22 and item lies in this interval, therefore it value is 25 .
2. Continuous series:
Procedure:
(i) Here data is given in the form of a frequency table with class interval.
(ii) Cumulative frequencies are found out for each value.
(iii) Median class is then calculated, where cumulative frequency ![]() lies is called median class.
lies is called median class.
(iv) Now median is calculated by applying the following formula.

Example 1. Find the median & median class of the data given below:
x | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
f | 4 | 11 | 19 | 14 | 0 | 2 |
Solution
Class | Mid-value (x) | f | c.f. |
15-25 | 20 | 4 | 4 |
25-35 | 30 | 11 | 15 |
35-45 | 40 | 19 | 34 |
45-55 | 50 | 14 | 48 |
55-65 | 60 | 0 | 48 |
65-75 | 70 | 2 | 50 |
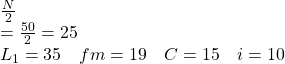
It is more than cumulative frequency 15 , but is less than the of. 34 . Hence the median clas is 35-45.
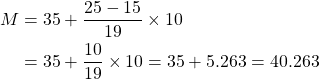
Median class 35-45.
Advantages and Disadvantages of Median:
Advantages:
(1) Like mean, the median can also be easily calculated and it is very easy to understand.
(2) It can be located by simple inspection in many cases.
(3) It is not affected by a few very large or very small observations and as such is more representative than arithmetic average.
(4) Grouped frequency distributions with classes of unequal width or with open end classes do not pose any problem in calculating the value of median ; this is an added advantage over A M.
(5) Its value can be computed graphically but A.M. cannot be calculated graphically.
(6) It is the only average to be used while dealing with qualitative data viz, intelligence, beauty, honesty etc, since it is possible to rank the individuals possessing these characteristics in some order. Thus it is a helpful measure of central tendency to qualitative data in psychological and social studies.
Disadvantages:
(1) For calculating median we need to arrange the data in order of magnitude; it is sometimes very tedious.
(2) It is not suitable for further mathematical treatment. We cannot compute the median of the composite group when the medians of several groups of observations are given.
(3) The median in some cases is a fair estimation but not an exact one according to the definition.
(4) Median is a positional average ; hence, it is not based on the values of all the observations.
(5) Median is relatively less stable than arithmetic mean because it is affected to a great extent by sampling fluctuations.
(6) Median would be an unsuitable average in situations where large or small observations in a series receive greater importance.

Leave a Reply