Geometric Mean (G.M.): Definition, Formula, Calculation, A-Z

5/5 - (6 votes)

Table of Contents

Definition:

Geometric mean of a set of n values of a variable gives a measure of their central tendency and is equal to the nth root of their product. Evidently, the geometric mean is not defined if one observation is zero or negative.

If G be the geometric mean of n values x₁, x₂, …, x_nof a variable x, then by definition,

Formula of Geometric Mean:

$G=\sqrt[n]{x_{1} \cdot x_{2} \ldots x_{n}}=\left(x_{1} \cdot x_{2} \ldots x_{n}\right)^{\frac{1}{n}}$

Example 1 . Calculate the GM of 4, 8, 16

Solution

$G=\sqrt[3]{4 \times 8 \times 16}=\left(2^{2} \times 2^{3} \times 2^{4}\right)^{\frac{1}{3}}\\ =\left(2^{9}\right)^{\frac{1}{3}}=2^{3}=8$

G.M.of weighted data :

let x₁, x₂, …, x_n be n different values assumed by a variable x with respective frequencies f₁, f₂ ,… , f_n. then the gm of x is defined as

$G=\left(x_{1}^{f_{1}}, x_{2}^{f_{2}} \ldots x_{n}^{f_{n}}\right)^{\frac{1}{N}},\text{where} N=\sum f_{i}$

G.M. of the group of data:

here all the observations are assumed to be clustered at the mid-points otfthre respective classes. thus, if x₁, x₂, …, x_n be respective mid-values of n different classes, having respective frequencies f₁, f₂,…, f_n. gm is defined as,

$G = ({x}_{1}{}^{{f}_{1}} . {x}_{2}{}^{{f}_{2}} ... {x}_{n}{}^{{f}_{n}}{ )}^{\frac{1}{n}}, where N = \sum{f}$

G.M. of Composite Group :

For two groups:

$G = ({G}_{1}{}^{{n}_{1}} . {G}_{2}{}^{{n}_{2}}{)}^{\frac{1}{{n}_{1} + {n}_{2}}}$

For there groups:

$G = ({G}_{1}{}^{{n}_{1}} . {G}_{2}{}^{{n}_{2}} . {G}_{3}{}^{{n}_{3}}{)}^{\frac{1}{{n}_{1} + {n}_{2} + {n}_{3}}}$

Important Properties of G.M.

The logarithm of the GM of a set of numbers is equal to the am of the logarithm of those numbers.

Proof : The GM of a set of numbers x₁, x₂, …, x_n with frequencies f₁, f₂, …, f_n is defined as

$G=\left(x_{1}^{f_{1}}, x_{2}^{f_{2}} \ldots x_{n}^{f_{n}}\right)^{\frac{1}{N}},\text{where} N=\sum f_{i}$

or,

$\begin{aligned} \log G &=\frac{1}{N} \log \left(x_{1}^{f_{1}} \cdot x_{2}^{f_{2}} \ldots x_{n}^{f_{n}}\right) \\ &=\frac{1}{N}\left(\log x_{1}^{f_{1}}+\log x_{2}^{f_{2}}+\ldots+\log x_{n}^{f_{n}}\right) \\ &=\frac{1}{N}\left(f_{1} \log x_{1}+f_{2} \log x_{2}+\ldots+f_{n} \log x_{n}\right)\\&=\frac{1}{N}\sum_{i=1}^{n} f_{i} \log x_{i}\end{aligned}$

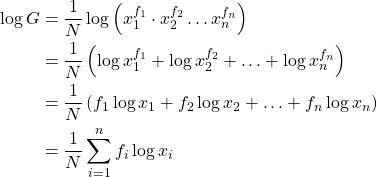
Advantages and Disadvantages of Geometric Mean:

Advantages:

Geometric mean possesses the following advantages as a statistical average:

(1) It is based on all the observations as in the case of A.M.

(2) It is rigidly defined; hence, it always possesses a definite value.

(3) It is capable of algebraic treatment.

(4) It is not very much affected by one or two very large or very small values of the variable. In this respect, it is better than the arithmetic mean.

(5) This form of average is very useful for averaging rates, ratios, and percentages.

(6) It is not affected to a great extent by fluctuations of sampling.

Disadvantages:

In spite of all these advantages the uses of G.M. as an average is limited because of the following major drawbacks :

(1) Its concept is not readily understood by common people.

(2) Because of its abstract mathematical character it is very difficult to calculate the value of G.M. for a non-mathematical person.

(3) The value of G.M. may not be an actual value of the variable.

(4) If any value of the variable is zero, geometric mean becomes zero; again, its value becomes imaginary when one of the variable values is negative. In these cases, the geometric mean is not defined.

Geometric Mean (G.M.): Definition, Formula, Calculation, A-Z

Definition: